.To determine the structure of an assembly of atoms, we need to solve the Schrödinger equation for both the ions and electrons. It is impossible to give an exact solution: progress can only be made if a set of approximations are made.
The first is due to Born and Oppenheimer who argue that, since the
nuclear masses are so much larger than those of the electrons, then we
can treat the nuclear motion classically and reduce the
Schrödinger equation to one only involving the electrons moving
in a potential of fixed nuclear sites denoted by R. The
solution of this equation is the structural potential energy
E(R). To determine dynamical quantities like vibrational
frequencies and diffusion barriers, we need then to solve the
classical problem of the nuclei moving in the force field .
Let us now consider the Schrödinger equation of the electrons
in a field of frozen nuclei. This equation still cannot be solved
exactly because of the inter-electronic Coulomb terms, 
. If these terms were neglected, then the
Schrödinger equation is separable and the exact wavefunction can
be written down as a sum of product orbitals 
where 
are the eigenfunctions of the one-electron
Hamiltonian. Of course, we must require that the total wavefunction is
antisymmetric and this can be achieved by a suitable sum over the
product orbitals. For, example for the H 
molecule, the
antisymmetric wavefunction is
This type of wavefunction is called a Slater determinant and is
specified by the electronic configuration, ie. a listing of the
orbitals 
occupied by the N electrons.
The neglect of the electron-electron interaction term is too
extreme to make this theory useful and various attempts have been made
to take this interaction into account. There are two principal
schemes: Hartree-Fock (HF) and density functional theory (DFT). Both
of these replace the electrostatic potential acting on electron
i by the other electrons, ie. 
by an
average over the positions of the other electrons. Thus this potential
becomes 
. Clearly the Schrödinger equation is then
separable and we can write the wavefunction as a Slater
determinant. In these theories, the effective potential is composed of
two terms: the Hartree potential 
and the
exchange-correlation potential 
. The former is
the electrostatic potential due to the electron density of charge
n(r) at point r. The density is determined by the
probability of finding a electron at the point, or
Here, the sum is over the occupied orbitals. The
exchange-correlation potential differs in the two theories. In HF, it
is a complicated function determined by all the orbitals . In DFT, it is rigorously determined only by the
electron density. This is an important result but the precise
dependence on density is not known except for a particular problem:
the homogeneous electron gas. In this case, the equations have been
solved numerically and the dependence of 
on n is
known exactly. For any other problem where the electron density varies
throughout space, we assume that at point
r is given by the homogeneous electron gas value involving the
density n(r) at the same point r. This is called
local density functional (LDF) theory. For high electron densities, it
can be shown that is proportional to 
and thus in
LDF theory is also proportional to 
. For
lower densities, can still be written down but is given by a
more complicated expression.
AIMPRO uses LDF theory and thus the electron density is a quantity of fundamental significance.
The problem has now been reduced to a one-electron one involving
the interaction of the electron with all the ions together with 
. Not all the electrons need be considered. Electrons
are divided into two groups: core and valence electrons. The former
are bound close to the ions and do not play a part in bonding. It is
highly advantageous to remove these from the theory. This can be done
through the use of the pseudopotential. For example, in Si the
1s, 2s, and 2p electrons are regarded as part of
the core while the 3s and 3p electrons are part of the
valence shell. The four bonds associated with each Si atom in the bulk
arise from these four valence electrons. The pseudopotential is
constructed by insisting that it has exactly the same valence energy
levels as the true atomic potential, ie. the 3s and
3p and even the 3d levels are the same (the 3d
levels are required because these orbitals are occupied to some extent
in the solid). Moreover, the corresponding pseudo-wavefunctions are
exactly equal to the true wavefunctions outside a core whose size
depends on the identity of the atom. Inside the core, the
pseudo-wavefunctions are not equal to the true valence ones but are
very smooth nodeless functions which are easy to represent
mathematically. The true 3s and 3p wavefunctions of Si
oscillate inside the core and are rather difficult to represent
mathematically. Fig. 1 shows these functions for Ni.
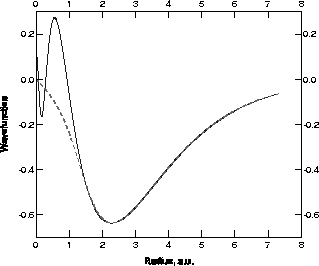
Figure: The 4s (full) and pseudo- (dashed)
radial wavefunction (a.u.) for the Ni atom.
The crucial point is that the pseudopotentials have no core states at all! The lowest bound state solutions are the valence energy eigenvalues and, as stated above, these are the same as the true valence energy levels. The pseudopotential has the great virtue of making the treatment of Ge say no more difficult than carbon. AIMPRO uses the pseudopotentials due to Bachelet, Hamann and Schlüter (BHS) who have given tables for all the elements from H to Pu.
Despite these great simplifications, we are still confronted with a formidable problem. We need to solve the eigenvalue problem:
Here H includes the kinetic energy, the sum of the
pseudopotentials for all the ions present, and the effective potential
which depends on the density of electrons
n(r). To proceed we expand the wavefunction in terms of
a basis 
. Thus
Two choices of 
are often made: plane waves and Cartesian
Gaussian orbitals. Using the first is equivalent to making a Fourier
transform of the wavefunction. This has problems with certain
elements, eg. first row, transition and rare-earth ones
where the wavefunction varies rapidly and a great number of plane
waves are required. AIMPRO uses Cartesian Gaussian orbitals of the
form
when centred at the origin. In practice, they are centred at the
nuclei and sometimes at bond centres sites between the nuclei. If 
then the orbitals are simply spherically symmetric
Gaussian functions sometimes called s-Gaussian orbitals. If one
of the 
is unity, and the others zero, then the functions are
p-Gaussian orbitals while if the sum of the is 2,
the set of six orbitals generate five d-orbitals and one
s orbital. The great advantage of Gaussian orbitals is that
analytical expressions can be given for all the integrals.
We now have to solve the equations
The next step is to multiple this equation through by 
and integrate over r. This reduces the
differential equation to a set of matrix equations:
which can be solved by matrix methods. 
and 
are matrix elements of the Hamiltonian and the overlap
respectively.
Once this equation has been solved we can generate the output charge density
In general this is not equal to the charge density used to generate
the effective potential . Of course,
this is wrong and we need to devise a scheme whereby the input charge
density, which is used to construct , is equal to
the output density. This is usually carried out by an iterative
procedure and the process of achieving equality in the densities is
called the self-consistent cycle.
AIMPRO uses an internal representation of the charge density by
expanding it in a basis of s-Gaussian functions 
. Thus
The particular exponents of the Gaussian 
together with
the exponents on the basis functions have been
calculated for atoms and given in a single data file called
"bhs.lib".
Once the self-consistent density has been found, the structural
energy E(R) can be evaluated. We then compute he forces
on each atom from 
and move the atoms until this energy is a
minimum and these forces vanish. This is called relaxing the assembly
of atoms.
The user of AIMPRO needs to provide 1) the positions of the atoms
in the cluster (in atomic units); 2) the basis to be used for the
wavefunction and charge density; 3) the electronic configuration; 4)
the identities of the atoms which are to be relaxed. The output gives
the energy, electronic levels 
, and positions
of the atoms. More specialised output is available.